注意:此页面搜索的是所有试题
西南石油大学土木工程施工与组织(专升本)
若函数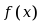 与
与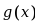 均在
均在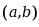 内可导,且
内可导,且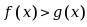 ,则在
,则在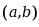 内必有
内必有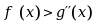 .( )
.( )
·正确
·错误
若初等函数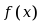 在
在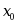 处及其邻域内有定义,则
处及其邻域内有定义,则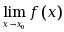 一定存在.( )
一定存在.( )
·正确
·错误
若极限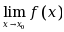 与
与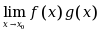 都存在,则极限
都存在,则极限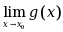 必也存在. ( )
必也存在. ( )
·正确
·错误
设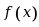 的一个原函数是
的一个原函数是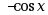 , 则
, 则 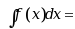 ( )
( )
·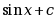
·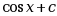
·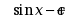
·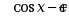
函数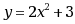 在区间
在区间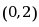 内 ( )
内 ( )
·有极值
·有最大值
·单调递增
·单调递减
设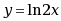 ,则
,则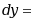 ( )
( )
·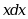
·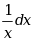
·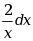
·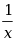
设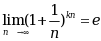 ,则
,则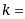 ( )
( )
·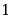
·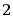
·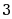
·
函数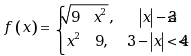 ,则
,则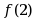 的值是( )
的值是( )
·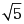
·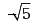
·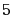
·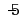
二次积分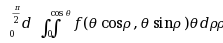 可以写成___________. ( )
可以写成___________. ( )
·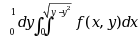
·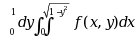
·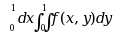
·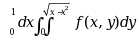
设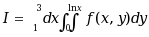 , 改变积分次序, 则
, 改变积分次序, 则 ( )
( )
·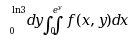
·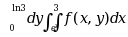
·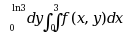
·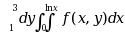
二元函数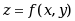 在点
在点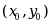 处满足关系( ).
处满足关系( ).
·可微(指全微分存在)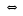 可导(指偏导数存在)
可导(指偏导数存在)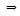 连续;
连续;
·可微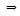 可导
可导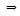 连续;
连续;
·可微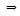 可导, 或可微
可导, 或可微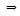 连续, 但可导不一定连续;
连续, 但可导不一定连续;
·可导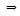 连续, 但可导不一定可微.
连续, 但可导不一定可微.
函数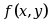 在点
在点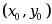 处偏导数存在是函数在该点可微分的 ( ).
处偏导数存在是函数在该点可微分的 ( ).
·充分而不必要条件;
·必要而不充分条件;
·必要而且充分条件;
·既不必要也不充分条件.
设函数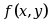 在点
在点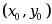 处连续是函数在该点可偏导的 ( )
处连续是函数在该点可偏导的 ( )
·充分而不必要条件;
·必要而不充分条件;
·必要而且充分条件;
·既不必要也不充分条件.
级数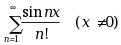 , 则该级数( )
, 则该级数( )
·是发散级数
·是绝对收敛级数
·是条件收敛级数
·可能收敛也可能发散
设幂级数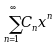 在点
在点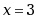 处收敛, 则该级数在点
处收敛, 则该级数在点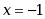 处( )
处( )
·绝对收敛
·条件收敛
·发散
·敛散性不定
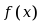 与
与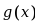 均在
均在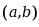 内可导,且
内可导,且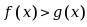 ,则在
,则在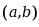 内必有
内必有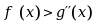 .( )
.( )·正确
·错误
若初等函数
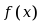 在
在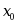 处及其邻域内有定义,则
处及其邻域内有定义,则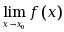 一定存在.( )
一定存在.( )·正确
·错误
若极限
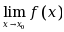 与
与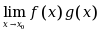 都存在,则极限
都存在,则极限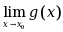 必也存在. ( )
必也存在. ( )·正确
·错误
设
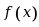 的一个原函数是
的一个原函数是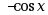 , 则
, 则 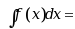 ( )
( )·
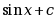
·
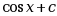
·
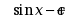
·
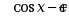
函数
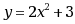 在区间
在区间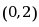 内 ( )
内 ( )·有极值
·有最大值
·单调递增
·单调递减
设
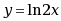 ,则
,则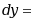 ( )
( )·
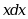
·
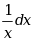
·
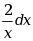
·
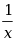
设
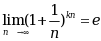 ,则
,则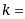 ( )
( )·
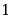
·
·
·
函数
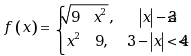 ,则
,则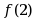 的值是( )
的值是( )·
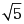
·
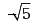
·
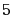
·
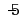
二次积分
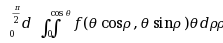 可以写成___________. ( )
可以写成___________. ( )·
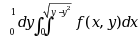
·
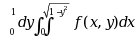
·
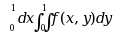
·
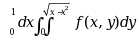
设
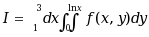 , 改变积分次序, 则
, 改变积分次序, 则 ( )
( )·
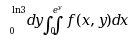
·
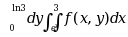
·
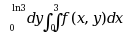
·
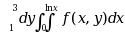
二元函数
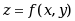 在点
在点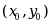 处满足关系( ).
处满足关系( ).·可微(指全微分存在)
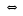 可导(指偏导数存在)
可导(指偏导数存在)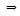 连续;
连续;·可微
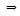 可导
可导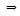 连续;
连续;·可微
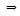 可导, 或可微
可导, 或可微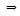 连续, 但可导不一定连续;
连续, 但可导不一定连续;·可导
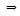 连续, 但可导不一定可微.
连续, 但可导不一定可微.函数
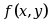 在点
在点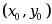 处偏导数存在是函数在该点可微分的 ( ).
处偏导数存在是函数在该点可微分的 ( ).·充分而不必要条件;
·必要而不充分条件;
·必要而且充分条件;
·既不必要也不充分条件.
设函数
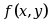 在点
在点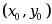 处连续是函数在该点可偏导的 ( )
处连续是函数在该点可偏导的 ( )·充分而不必要条件;
·必要而不充分条件;
·必要而且充分条件;
·既不必要也不充分条件.
级数
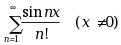 , 则该级数( )
, 则该级数( )·是发散级数
·是绝对收敛级数
·是条件收敛级数
·可能收敛也可能发散
设幂级数
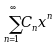 在点
在点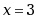 处收敛, 则该级数在点
处收敛, 则该级数在点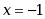 处( )
处( )·绝对收敛
·条件收敛
·发散
·敛散性不定