注意：此页面搜索的是所有试题
西南石油大学土木工程施工与组织(专升本)
基孔制中的基准孔的基本偏差代号为( )。
·h
·H
·A
·a
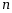阶线性齐次微分方程的所有解( ).
·构成一个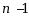
线性空间
·构成一个
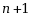维线性空间
·构成一个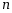
维线性空间
·不能构成一个线性空间
通解为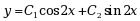
的微分方程是( ).
·
·
·
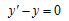
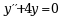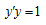
·<img src="https://s3.cn-north-1.amazonaws.com.cn/qingshuxuetang/examination/imgUplod/155116704195882cefed23e864e02a64f2f1850aada3dimage47.png"
方程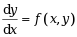
的任一饱和解的最大存在区间必是一个( ).
·闭区间
·开区间
·左开右闭区间
·左闭右开区间
设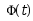
和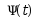
是微分方程组
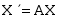的基解矩阵,则有( )
·
;
·
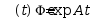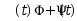也是基解矩阵;
·
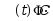也基解矩阵,这里
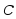是
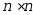常数矩阵;
·
.
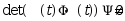5阶线性非齐次微分方程的7个解必定( ).
· 可构成方程的一个基本解组;
· 线性相关;
· 朗斯基行列式恒不为零;
· 线性无关.
初值问题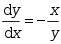
满足初始条件
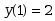的解是( )
·
;
·
;
·
;
·
.
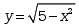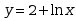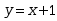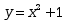已知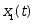
是微分方程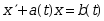
的一个特解,
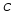是任意常数,则该方程的通解为( )
·
;
·
;
·
;
·
.
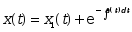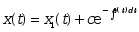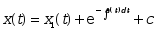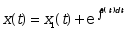下列方程中为常微分方程的是( )
·
·
·
·
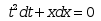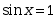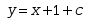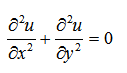
下列微分方程是线性的是( )
·
·
·
·
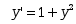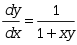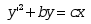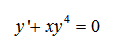
下列函数组在定义域内线性无关的是( )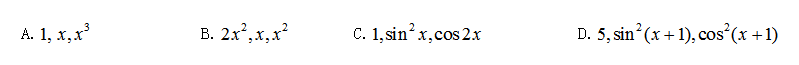
·A
·B
·C
·D
方程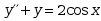
特解的形状为( )
·
· 
·
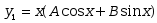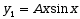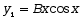·<img src="https://s3.cn-north-1.amazonaws.com.cn/qingshuxuetang/examination/imgUplod/16557157802192ea788d39b33404d8b92c5a9179bdb7aimage17.png"
设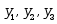
是二阶线性微分方程
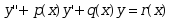的三个不同的特解,且
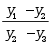不是常数,则该方程的通解为( )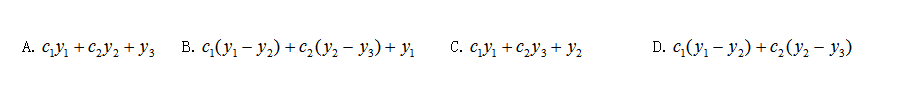
·A
·B
·C
·D
设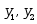
是方程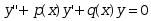
的两个特解,则
(
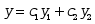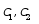为任意常数)( )
·是此方程的通解
·是此方程的特解
·不一定是该方程的解
·是该方程的解
方程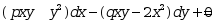
是全微分的充要条件是( )
·
·
·
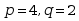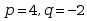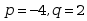·<img src="https://s3.cn-north-1.amazonaws.com.cn/qingshuxuetang/examination/imgUplod/165571578081006782e472c094cdbb4f1458ed1b3050fimage33.png"
·h
·H
·A
·a
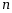阶线性齐次微分方程的所有解( ).·构成一个
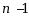线性空间·构成一个
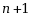维线性空间·构成一个
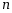维线性空间·不能构成一个线性空间
通解为
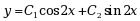的微分方程是( ).·
·
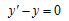
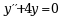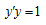
··<img src="https://s3.cn-north-1.amazonaws.com.cn/qingshuxuetang/examination/imgUplod/155116704195882cefed23e864e02a64f2f1850aada3dimage47.png"
方程
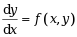的任一饱和解的最大存在区间必是一个( ).·闭区间
·开区间
·左开右闭区间
·左闭右开区间
设
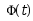和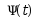是微分方程组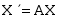的基解矩阵,则有( )·
;·
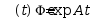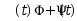也是基解矩阵;·
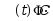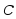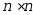也基解矩阵,这里是常数矩阵;·
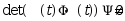.5阶线性非齐次微分方程的7个解必定( ).
· 可构成方程的一个基本解组;
· 线性相关;
· 朗斯基行列式恒不为零;
· 线性无关.
初值问题
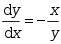满足初始条件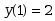的解是( )·
;·
;·
;·
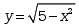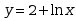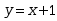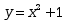.已知
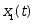是微分方程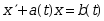的一个特解,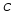是任意常数,则该方程的通解为( )·
;·
;·
;·
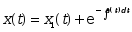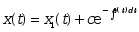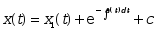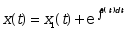.下列方程中为常微分方程的是( )
·
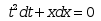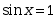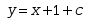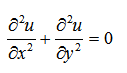
···下列微分方程是线性的是( )
·
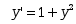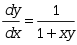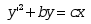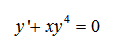
···下列函数组在定义域内线性无关的是( )
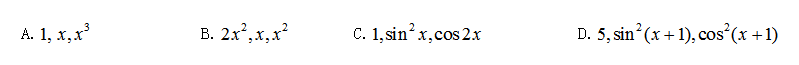
·A
·B
·C
·D
方程
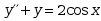特解的形状为( )·
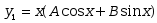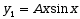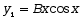· ··<img src="https://s3.cn-north-1.amazonaws.com.cn/qingshuxuetang/examination/imgUplod/16557157802192ea788d39b33404d8b92c5a9179bdb7aimage17.png"设
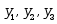是二阶线性微分方程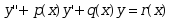的三个不同的特解,且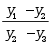不是常数,则该方程的通解为( )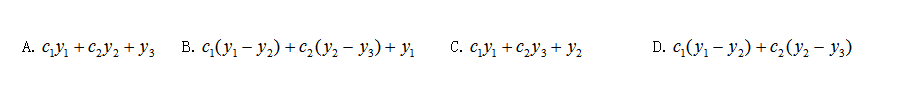·A
·B
·C
·D
设
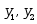是方程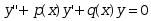的两个特解,则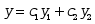(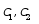为任意常数)( )·是此方程的通解
·是此方程的特解
·不一定是该方程的解
·是该方程的解
方程
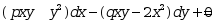是全微分的充要条件是( )·
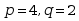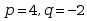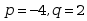···<img src="https://s3.cn-north-1.amazonaws.com.cn/qingshuxuetang/examination/imgUplod/165571578081006782e472c094cdbb4f1458ed1b3050fimage33.png"