注意：此页面搜索的是所有试题
佳木斯大学语言治疗学
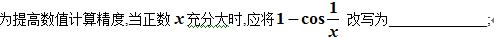以下答案中那几项是正确的？·
·
·
·
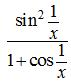
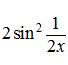
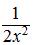
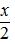
在科学与工程计算中,估计计算结果的精确度是十分重要的工作,而影响精确度的因素是各种各样的误差.按照它们的来源,误差可以分为以下哪几种( )
·模型误差
·观测误差
·截断误差
·舍入误差
按照一般的情况,指出选用算法时应遵循的一般原则是( )。
·要尽量简化计算步骤以减少运算次数
·要防止大数“吃掉”小数
·尽量避免相近的数相减
·除法运算中应尽量避免除数的绝对值远远小于被除数的绝对值
·选用数值稳定性好的公式,以控制舍入误差的传播
求隔根区间的方法有( )。
·描图法
·逐步搜索法
·二分法
·迭代法
设为区间[a,b]上的连续函数,且已知点
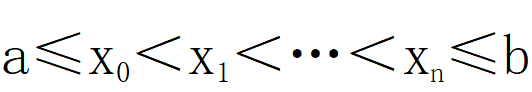上的函数值为
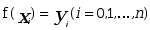,若存在一个简单函数φ(x),使
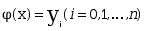,则下列说法正确的是( )。·φ(x)称为f(x)的插值函数,f(x) 称为被插值函数
·点
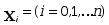称为插值节点·条件
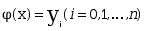称为插值条件·所在区间[a,b]称为插值区间,求插值函数φ(x)的问题(方法)称为插值问题(方法)
下列关于局部截断误差和整体截断误差的说法正确的是( )。
·局部与整体截断误差是方法的理论误差
·欧拉法的局部截断误差为
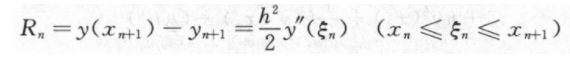
·梯形法的局部截断误差为
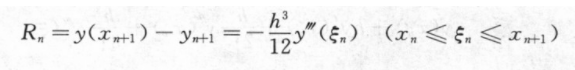
·除了用数值积分方法推导局部截断误差外,泰勒展开方法也是推导局部截断误差的常用方法
若某一数值方法的局部截断误差为Rn=O(hp+1),p为正整数,则称这个数值方法为p阶方法,或者说该方法具有p阶精度,根据这个定义,可以知晓的是( )。
·欧拉方法是一阶方法
·欧拉方法是二阶方法
·梯形法是二阶方法
·欧拉预估-校正法是二阶方法
下列关于偏微分方程的数值解法的说法正确的有( )。
·偏微分方程定解问题的数值解法之一是差分解法
·偏微分方程定解问题的数值解法之二是有限元方法
·差分解法的基本思想是:在偏微分方程中,用差商(均差)代替偏导数,把偏微分方程定解问题转化为求解线性代数方程问题,从而得到定解问题的解函数在离散点的近似值
·线性代数方程称为差分方程,差分方程的解称为偏微分方程定解问题的数值解.
取“3.15”作为π的近似值,则下列计算结果正确的是( )。
·绝对误差为:
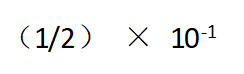
·相对误差为:
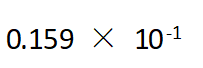
·有效数字为:1位
·有效数字为:2位
取“22/7”作为π的近似值,则下列计算结果正确的是( )。
·绝对误差为:
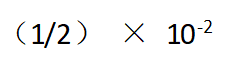
·相对误差为:
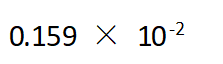
·有效数字为:3位
·有效数字为:2位
取“355/113”作为π的近似值,则下列计算结果正确的是( )。
·绝对误差为:
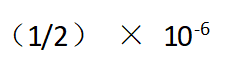
·相对误差为:
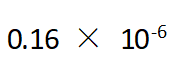
·有效数字为:7位
·有效数字为:6位
方程
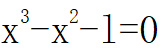在1.5附近有根,把方程写成4种不同的等价形式,并建立相应的迭代公式,具体如图,则判断每种迭代公式产生的数列在1.5附近的收敛性,正确的是( )。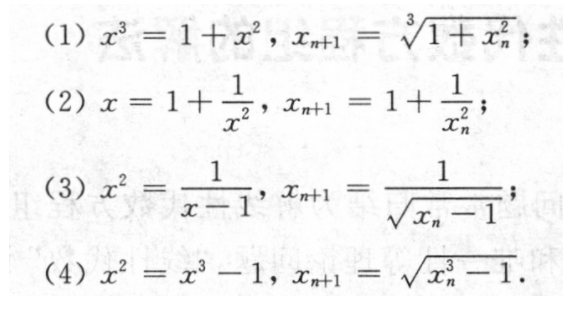
·(1)收敛
·(2)收敛
·(3)发散
·(4)发散
下列计算结果正确的是( )。
·用迭代法求
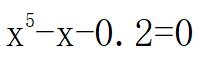的正根,准确到小数点后第5位的值为:a≈1.04476·用迭代法求
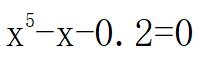的正根,准确到小数点后第5位的值为:a≈1.04000·用迭代法求方程
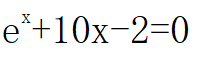的根,要求精度为
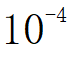的值为:a≈0.0905·用迭代法求方程
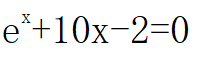的根,要求精度为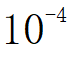的值为:a≈0.0900关于方程cosx+sinx-4x=0,有如下说法,正确的是( )。
·该方程的有一个根
·该方程的有二个根
·隔根区间为[0,π/4]
·收敛的迭代公式为:
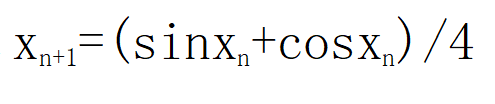
下列方程表述正确的是( )。
·方程x=f(x)的根的牛顿迭代格式为:<img src="https://s3.cn-north-1.amazonaws.com.cn/qingshuxuetang/examination/imgUplod/166792179281118375949b6ef477d96ecd9704331fc35image24.png"