注意:此页面搜索的是所有试题
佳木斯大学语言治疗学
设A、B均为方阵,则下列结论中正确的是( )
·若|AB|=0,则A=0或B=0
·若|AB|=0,则|A|=0或|B|=0
·若AB=0,则A=0或B=0
·若AB≠0,则|A|≠0或|B|≠0
设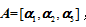 其中
其中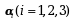 是三维列向量,若|A|=1,则
是三维列向量,若|A|=1,则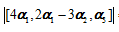 =( )
=( )
·-24
·-12
·12
·24
设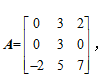 ,则|A|=( )
,则|A|=( )
·-12
·0
·12
·21
设A为3阶矩阵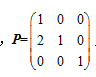 ,则用P左乘A,相当于将A( )
,则用P左乘A,相当于将A( )
·第1行的2倍加到第2行
·第1列的2倍加到第2列
·第2行的2倍加到第1行
·第2列的2倍加到第1列
设A为3阶矩阵,且|A|=3,则|(-A)-1|=( )
·-3
·-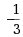
·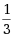
·3
设行列式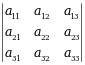 =2,则
=2,则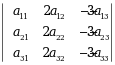 =( )
=( )
·-12
·-6
·6
·12
设矩阵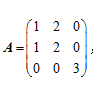 ,则A*中位于第1行第2列的元素是( )
,则A*中位于第1行第2列的元素是( )
·-6
·-3
·3
·6
实二次型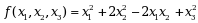 则f是( )
则f是( )
·负定
·正定
·半正定
·不定
二次型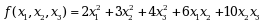 的矩阵是( )
的矩阵是( )
·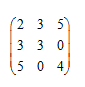
·
·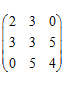
·
设A是n阶方阵,且|5A+3E|=0,则A必有一个特征值为( )
·-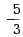
·-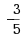
·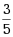
·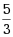
若矩阵A与对角矩阵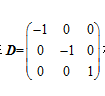 相似,则A3=( )
相似,则A3=( )
·E
·D
·-E
·A
设A、B为同阶方阵,且秩(A)=秩(B),则( )
·A与B等阶
·A与B合同
·|A|=|B|
·A与B相似
设三阶矩阵A有特征值0、1、2,其对应特征向量分别为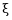 1、
1、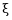 2、
2、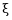 3,令P=[
3,令P=[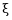 3,
3,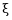 1,
1, 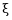 2],则P-1AP=( )
2],则P-1AP=( )
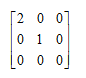
·
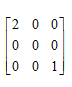
·
·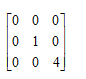
·
若A为正交矩阵,则下列矩阵中不是正交阵的是( )
·A-1
·2A
·A2
·AT
设4阶矩阵A的秩为3,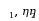 为非齐次线性方程组Ax=b的两个不同的解,c为任意常数,则该方程组的通解为( )
为非齐次线性方程组Ax=b的两个不同的解,c为任意常数,则该方程组的通解为( )
·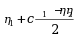
·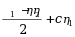
·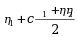
·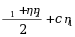
·若|AB|=0,则A=0或B=0
·若|AB|=0,则|A|=0或|B|=0
·若AB=0,则A=0或B=0
·若AB≠0,则|A|≠0或|B|≠0
设
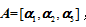 其中
其中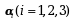 是三维列向量,若|A|=1,则
是三维列向量,若|A|=1,则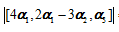 =( )
=( )·-24
·-12
·12
·24
设
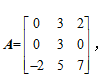 ,则|A|=( )
,则|A|=( )·-12
·0
·12
·21
设A为3阶矩阵
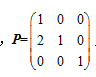 ,则用P左乘A,相当于将A( )
,则用P左乘A,相当于将A( )·第1行的2倍加到第2行
·第1列的2倍加到第2列
·第2行的2倍加到第1行
·第2列的2倍加到第1列
设A为3阶矩阵,且|A|=3,则|(-A)-1|=( )
·-3
·-
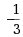
·
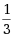
·3
设行列式
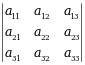 =2,则
=2,则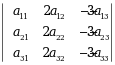 =( )
=( )·-12
·-6
·6
·12
设矩阵
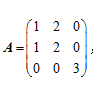 ,则A*中位于第1行第2列的元素是( )
,则A*中位于第1行第2列的元素是( )·-6
·-3
·3
·6
实二次型
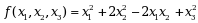 则f是( )
则f是( )·负定
·正定
·半正定
·不定
二次型
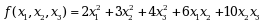 的矩阵是( )
的矩阵是( )·
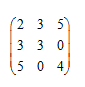
·

·
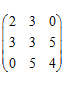
·

设A是n阶方阵,且|5A+3E|=0,则A必有一个特征值为( )
·-
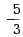
·-
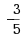
·
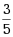
·
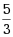
若矩阵A与对角矩阵
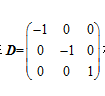 相似,则A3=( )
相似,则A3=( )·E
·D
·-E
·A
设A、B为同阶方阵,且秩(A)=秩(B),则( )
·A与B等阶
·A与B合同
·|A|=|B|
·A与B相似
设三阶矩阵A有特征值0、1、2,其对应特征向量分别为
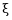 1、
1、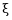 2、
2、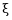 3,令P=[
3,令P=[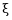 3,
3,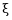 1,
1, 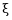 2],则P-1AP=( )
2],则P-1AP=( )·

·

·

·

若A为正交矩阵,则下列矩阵中不是正交阵的是( )
·A-1
·2A
·A2
·AT
设4阶矩阵A的秩为3,
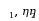 为非齐次线性方程组Ax=b的两个不同的解,c为任意常数,则该方程组的通解为( )
为非齐次线性方程组Ax=b的两个不同的解,c为任意常数,则该方程组的通解为( )·
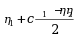
·
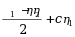
·
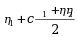
·