注意：此页面搜索的是所有试题
佳木斯大学语言治疗学
已知0<θ<,则双曲线C1:-=1与C2:-=1的( )
·实轴长相等
·虚轴长相等
·离心率相等
·焦距相等
设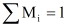
，则
（ ）
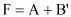·0
·x
·1
·2
设椭圆C1的离心率为,焦点在x轴上且长轴长为26,若曲线C2上的点到椭圆C1的两个焦点的距离的差的绝对值等于8,则曲线C2的标准方程为( )
·-=1
·-=1
·-=1
·-=1
若双曲线-=1渐近线上的一个动点P总在平面区域(x-m)2+y2≥16内,则实数m的取值范围是( )
·[-3,3]
·(-∞,-3]∪[3,+∞)
·[-5,5]
·(-∞,-5]∪[5,+∞)
抛物线的焦点为椭圆+=1的下焦点,顶点在椭圆中心,则抛物线方程为( )
·x2=-4y
·y2=-4x
·x2=-4y
·y2=-4x
已知抛物线y2=2px,以过焦点的弦为直径的圆与抛物线准线的位置关系是( )
·相离
·相交
·相切
·不确定
设M(x0,y0)为抛物线C:x2=8y上一点,F为抛物线C的焦点,以F为圆心、|FM|为半径的圆和抛物线C的准线相交,则y0的取值范围是( )
·(0,2)
·[0,2]
·(2,+∞)
·[2,+∞)
( ).
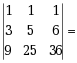·3
·5
·6
·8
下列矩阵中是正定矩阵的为( )
·
·
·
·
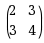
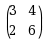
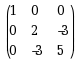
设A是实对称矩阵,C是实可逆矩阵,B=CTAC.则( )
·A与B相似
·A与B不等价
·A与B有相同的特征值
·A与B合同
设A是一个n(≥3)阶方阵,下列陈述中正确的是( )
·如存在数λ和向量α使Aα=λα,则α是A的属于特征值λ的特征向量
·如存在数λ和非零向量α,使(λE-A)α=0,则λ是A的特征值
·A的2个不同的特征值可以有同一个特征向量
·如λ1,λ2,λ3是A的3个互不相同的特征值,α1,α2,α3依次是A的属于λ1,λ2,λ3的特征向量,则α1,α2,α3有可能线性相关
设Ax=b是一非齐次线性方程组,η1,η2是其任意2个解,则下列结论错误的是( )
·η1+η2是Ax=0的一个解
·
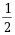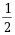η1+η2是Ax=b的一个解
·η1-η2是Ax=0的一个解
·2η1-η2是Ax=b的一个解
设两个向量组α1,α2,…,αs和β1,β2,…,βs均线性相关,则( )
·有不全为0的数λ1,λ2,…,λs使λ1α1+λ2α2+…+λsαs=0和λ1β1+λ2β2+…λsβs=0
·有不全为0的数λ1,λ2,…,λs使λ1(α1+β1)+λ2(α2+β2)+…+λs(αs+βs)=0
·有不全为0的数λ1,λ2,…,λs使λ1(α1-β1)+λ2(α2-β2)+…+λs(αs-βs)=0
·有不全为0的数λ1,λ2,…,λs和不全为0的数μ1,μ2,…,μs使λ1α1+λ2α2+…+λsαs=0和μ1β1+μ2β2+…+μsβs=0
设A是方阵,如有矩阵关系式AB=AC,则必有( )
·A =0
·B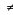
C时A=0
·A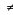0时B=C
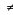·|A|0时B=C
设矩阵A=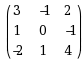
,A*是A的伴随矩阵,则A *中位于(1,2)的元素是( )
·–6
·6
·2
·–2
·实轴长相等
·虚轴长相等
·离心率相等
·焦距相等
设
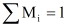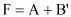，则（ ）·0
·x
·1
·2
设椭圆C1的离心率为,焦点在x轴上且长轴长为26,若曲线C2上的点到椭圆C1的两个焦点的距离的差的绝对值等于8,则曲线C2的标准方程为( )
·-=1
·-=1
·-=1
·-=1
若双曲线-=1渐近线上的一个动点P总在平面区域(x-m)2+y2≥16内,则实数m的取值范围是( )
·[-3,3]
·(-∞,-3]∪[3,+∞)
·[-5,5]
·(-∞,-5]∪[5,+∞)
抛物线的焦点为椭圆+=1的下焦点,顶点在椭圆中心,则抛物线方程为( )
·x2=-4y
·y2=-4x
·x2=-4y
·y2=-4x
已知抛物线y2=2px,以过焦点的弦为直径的圆与抛物线准线的位置关系是( )
·相离
·相交
·相切
·不确定
设M(x0,y0)为抛物线C:x2=8y上一点,F为抛物线C的焦点,以F为圆心、|FM|为半径的圆和抛物线C的准线相交,则y0的取值范围是( )
·(0,2)
·[0,2]
·(2,+∞)
·[2,+∞)
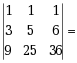( ).·3
·5
·6
·8
下列矩阵中是正定矩阵的为( )
·
·
·
·
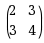
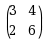
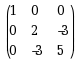
设A是实对称矩阵,C是实可逆矩阵,B=CTAC.则( )
·A与B相似
·A与B不等价
·A与B有相同的特征值
·A与B合同
设A是一个n(≥3)阶方阵,下列陈述中正确的是( )
·如存在数λ和向量α使Aα=λα,则α是A的属于特征值λ的特征向量
·如存在数λ和非零向量α,使(λE-A)α=0,则λ是A的特征值
·A的2个不同的特征值可以有同一个特征向量
·如λ1,λ2,λ3是A的3个互不相同的特征值,α1,α2,α3依次是A的属于λ1,λ2,λ3的特征向量,则α1,α2,α3有可能线性相关
设Ax=b是一非齐次线性方程组,η1,η2是其任意2个解,则下列结论错误的是( )
·η1+η2是Ax=0的一个解
·
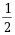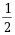η1+η2是Ax=b的一个解·η1-η2是Ax=0的一个解
·2η1-η2是Ax=b的一个解
设两个向量组α1,α2,…,αs和β1,β2,…,βs均线性相关,则( )
·有不全为0的数λ1,λ2,…,λs使λ1α1+λ2α2+…+λsαs=0和λ1β1+λ2β2+…λsβs=0
·有不全为0的数λ1,λ2,…,λs使λ1(α1+β1)+λ2(α2+β2)+…+λs(αs+βs)=0
·有不全为0的数λ1,λ2,…,λs使λ1(α1-β1)+λ2(α2-β2)+…+λs(αs-βs)=0
·有不全为0的数λ1,λ2,…,λs和不全为0的数μ1,μ2,…,μs使λ1α1+λ2α2+…+λsαs=0和μ1β1+μ2β2+…+μsβs=0
设A是方阵,如有矩阵关系式AB=AC,则必有( )
·A =0
·B
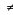C时A=0·A
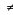0时B=C·|A|
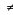0时B=C设矩阵A=
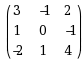,A*是A的伴随矩阵,则A *中位于(1,2)的元素是( )·–6
·6
·2
·–2