注意:此页面搜索的是所有试题
西南石油大学土木工程施工与组织(专升本)
经过点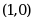 且切线斜率为
且切线斜率为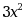 的曲线方程是( )。
的曲线方程是( )。
·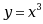 ;
;
·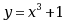 ;
;
·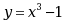 ;
;
·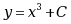 。
。
设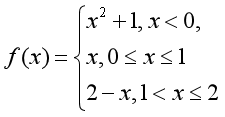 则
则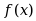 在( )
在( )
·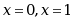 处都间断
处都间断
·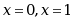 处都连续
处都连续
·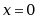 处间断,
处间断,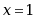 处连续
处连续
·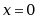 处连续,
处连续,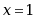 处间断
处间断
变量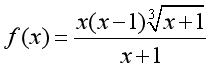 在变化过程为( )时为无穷大量。
在变化过程为( )时为无穷大量。
·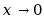
·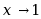
·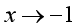
·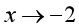
对于空间直线方程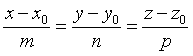 ,下列描述正确的是( )
,下列描述正确的是( )
·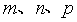 都不能为零
都不能为零
·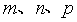 不能全为零
不能全为零
· 空间点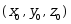 在该直线上
在该直线上
· 该直线与向量 垂直
垂直
下述命题不成立的是()
·闭区间上的连续函数必可积;
·闭区间上的有界函数必可积;
·闭区间上的单调函数必可积;
·闭区间上的逐段连续函数必可积.
设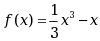 ,则
,则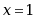 是
是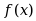 在
在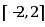 上的( )。
上的( )。
· 极小值点,但不是最小值点;
· 极小值点,也是最小值点;
· 极大值点,但不是最大值点;
· 极大值点,也是最大值点。
设函数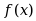 在
在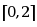 上连续,且在
上连续,且在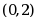 内
内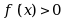 ,则下列不等式成立的是( )。
,则下列不等式成立的是( )。
·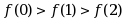 ;
;
·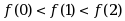 ;
;
·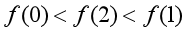
·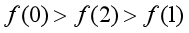
设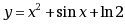 ,则
,则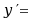 ( )。
( )。
·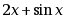 ;
;
·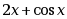 ;
;
·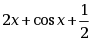 ;
;
·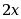 。
。
设函数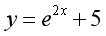 ,则
,则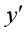 ( )
( )
·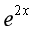
·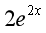
·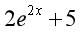
·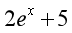
设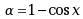 ,
,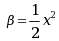 ,则当
,则当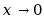 时( )。
时( )。
·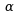 与
与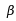 是同阶但不等价的无穷小;
是同阶但不等价的无穷小;
·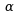 与
与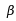 是等价的无穷小;
是等价的无穷小;
·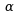 是
是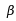 的高阶无穷小;
的高阶无穷小;
·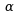 是
是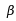 的低阶无穷小。
的低阶无穷小。
函数y=f(x),在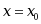 处,下列结论正确的是( )
处,下列结论正确的是( )
· 若函数在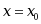 处连续,则函数在该点一定可导。
处连续,则函数在该点一定可导。
· 若函数在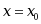 处可导,则函数在该点一定连续。
处可导,则函数在该点一定连续。
· 若函数在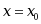 处不可导,则函数在该点一定不连续。
处不可导,则函数在该点一定不连续。
· 函数的连续与函数的可导是等价关系。
曲线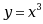 的拐点坐标是( )。
的拐点坐标是( )。
·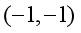 ;
;
·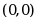 ;
;
·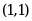 ;
;
·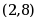 。
。
下列各对函数中相同的是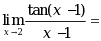 ( )
( )
· 0
·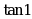
·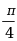
· 2
对二重积分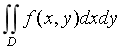 计算过程中,必须对积分区域
计算过程中,必须对积分区域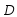 进行分块的情况有( )
进行分块的情况有( )
· 函数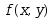 在区域
在区域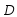 上是分片函数
上是分片函数
· 积分区域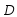 既非
既非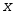 型又非
型又非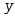 型
型
· 积分区域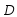 的边界线中有分段函数
的边界线中有分段函数
· 积分区域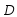 的边界线全部为曲线
的边界线全部为曲线
在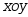 平面上与矢量
平面上与矢量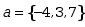 垂直的单位矢量是( )
垂直的单位矢量是( )
·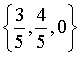
·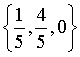
·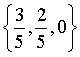
·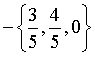
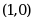 且切线斜率为
且切线斜率为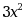 的曲线方程是( )。
的曲线方程是( )。·
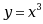 ;
;·
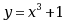 ;
;·
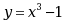 ;
;·
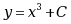 。
。设
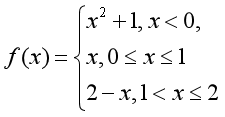 则
则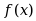 在( )
在( )·
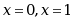 处都间断
处都间断·
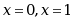 处都连续
处都连续·
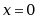 处间断,
处间断,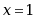 处连续
处连续·
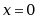 处连续,
处连续,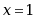 处间断
处间断变量
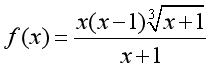 在变化过程为( )时为无穷大量。
在变化过程为( )时为无穷大量。·
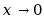
·
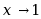
·
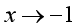
·
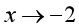
对于空间直线方程
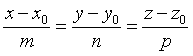 ,下列描述正确的是( )
,下列描述正确的是( )·
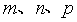 都不能为零
都不能为零·
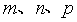 不能全为零
不能全为零· 空间点
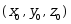 在该直线上
在该直线上· 该直线与向量
 垂直
垂直下述命题不成立的是()
·闭区间上的连续函数必可积;
·闭区间上的有界函数必可积;
·闭区间上的单调函数必可积;
·闭区间上的逐段连续函数必可积.
设
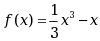 ,则
,则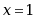 是
是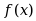 在
在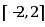 上的( )。
上的( )。· 极小值点,但不是最小值点;
· 极小值点,也是最小值点;
· 极大值点,但不是最大值点;
· 极大值点,也是最大值点。
设函数
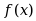 在
在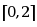 上连续,且在
上连续,且在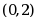 内
内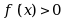 ,则下列不等式成立的是( )。
,则下列不等式成立的是( )。·
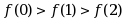 ;
;·
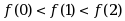 ;
;·
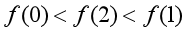
·
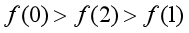
设
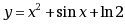 ,则
,则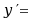 ( )。
( )。·
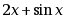 ;
;·
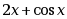 ;
;·
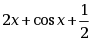 ;
;·
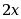 。
。设函数
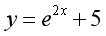 ,则
,则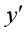 ( )
( )·
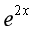
·
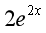
·
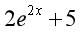
·
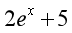
设
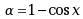 ,
,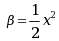 ,则当
,则当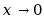 时( )。
时( )。·
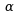 与
与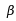 是同阶但不等价的无穷小;
是同阶但不等价的无穷小;·
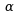 与
与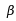 是等价的无穷小;
是等价的无穷小;·
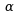 是
是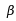 的高阶无穷小;
的高阶无穷小;·
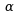 是
是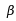 的低阶无穷小。
的低阶无穷小。函数y=f(x),在
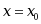 处,下列结论正确的是( )
处,下列结论正确的是( )· 若函数在
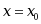 处连续,则函数在该点一定可导。
处连续,则函数在该点一定可导。· 若函数在
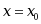 处可导,则函数在该点一定连续。
处可导,则函数在该点一定连续。· 若函数在
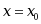 处不可导,则函数在该点一定不连续。
处不可导,则函数在该点一定不连续。· 函数的连续与函数的可导是等价关系。
曲线
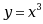 的拐点坐标是( )。
的拐点坐标是( )。·
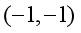 ;
;·
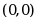 ;
;·
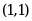 ;
;·
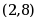 。
。下列各对函数中相同的是
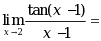 ( )
( )· 0
·
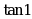
·
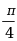
· 2
对二重积分
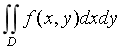 计算过程中,必须对积分区域
计算过程中,必须对积分区域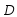 进行分块的情况有( )
进行分块的情况有( )· 函数
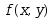 在区域
在区域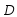 上是分片函数
上是分片函数· 积分区域
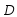 既非
既非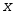 型又非
型又非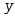 型
型· 积分区域
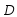 的边界线中有分段函数
的边界线中有分段函数· 积分区域
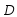 的边界线全部为曲线
的边界线全部为曲线在
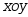 平面上与矢量
平面上与矢量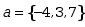 垂直的单位矢量是( )
垂直的单位矢量是( )·
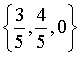
·
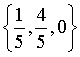
·
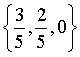
·