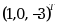注意:此页面搜索的是所有试题
川北医学院口腔医学院
已知 A=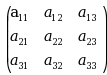 , B=
, B=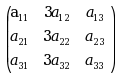 P=
P=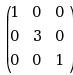 , Q=
, Q=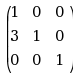 , 则 B=( )
, 则 B=( )
·PA
·AP
·QA
·AQ
已知 A 是一个 3×4 矩阵,下列命题中正确的是( )
·若矩阵 A 中所有 3 阶子式都为 0,则秩(A)=2
·若 A 中存在 2 阶子式不为 0,则秩(A)=2
·若秩(A)=2,则 A 中所有 3 阶子式都为 0
·若秩(A)=2,则 A 中所有 2 阶子式都不为 0
下列命题中错误的是( )
·只含有一个零向量的向量组线性相关
·由 3 个 2 维向量组成的向量组线性相关
·由一个非零向量组成的向量组线性相关
·两个成比例的向量组成的向量组线性相关
已知向量组α1,α2,α3线性无关,α1,α2,α3,β线性相关,则( )
·α1必能由α2,α3,β线性表出
·α2必能由α1,α3,β线性表出
·α3必能由α1,α2,β线性表出
·β必能由α1,α2,α3线性表出
设 A 为 m×矩阵,m≠n,则齐次线性方程组 Ax=0 只有零解的充分必要条件是 A 的秩( )
·小于 m
·等于 m
·小于 n
·等于 n
设 A 为可逆矩阵,则与 A 必有相同特征值的矩阵为( )
·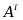
·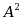
·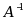
·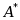
二次型 f(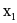 ,
,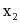 ,
,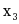 )=
)=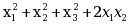 的正惯性指数为( )
的正惯性指数为( )
·0
·1
·2
·3
设行列式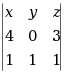 =1,则行列式
=1,则行列式 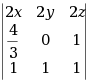 =( )
=( )
·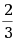
·1
·2
·
设 A,B,C 为同阶可逆方阵,则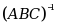 =( )
=( )
·
·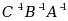
·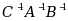
·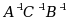
设 α 1, α 2, α 3, α 4是 4 维列向量,矩阵 A=( α 1, α 2, α 3, α 4).如果|A|=2,则|-2A|=( )
·-32
·-4
·4
·32
设 α 1, α 2, α 3, α 4 是三维实向量,则( )
·α 1, α 2, α 3, α 4一定线性无关
·α 1一定可由 α 2, α 3, α 4线性表出
·α 1, α 2, α 3, α 4一定线性相关
·α 1, α 2, α 3一定线性无关
向量组 α 1=(1,0,0), α 2=(1,1,0), α 3=(1,1,1)的秩为( )
·1
·2
·3
·4
设 A 是 4×6 矩阵,r( )=2,则齐次线性方程组 Ax=0 的基础解系中所含向量的个数是( )
·1
·2
·3
·4
设 A 是 m×矩阵,已知 Ax=0 只有零解,则以下结论正确的是( )
·m≥n
·Ax=b(其中 b 是 m 维实向量)必有唯一解
·r(A)=m
·Ax=0 存在基础解系
设矩阵 A=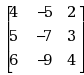 ,则以下向量中是 A 的特征向量的是( )
,则以下向量中是 A 的特征向量的是( )
·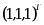
·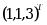
·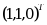
·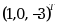
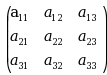 , B=
, B=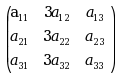 P=
P=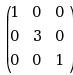 , Q=
, Q=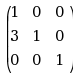 , 则 B=( )
, 则 B=( )·PA
·AP
·QA
·AQ
已知 A 是一个 3×4 矩阵,下列命题中正确的是( )
·若矩阵 A 中所有 3 阶子式都为 0,则秩(A)=2
·若 A 中存在 2 阶子式不为 0,则秩(A)=2
·若秩(A)=2,则 A 中所有 3 阶子式都为 0
·若秩(A)=2,则 A 中所有 2 阶子式都不为 0
下列命题中错误的是( )
·只含有一个零向量的向量组线性相关
·由 3 个 2 维向量组成的向量组线性相关
·由一个非零向量组成的向量组线性相关
·两个成比例的向量组成的向量组线性相关
已知向量组α1,α2,α3线性无关,α1,α2,α3,β线性相关,则( )
·α1必能由α2,α3,β线性表出
·α2必能由α1,α3,β线性表出
·α3必能由α1,α2,β线性表出
·β必能由α1,α2,α3线性表出
设 A 为 m×矩阵,m≠n,则齐次线性方程组 Ax=0 只有零解的充分必要条件是 A 的秩( )
·小于 m
·等于 m
·小于 n
·等于 n
设 A 为可逆矩阵,则与 A 必有相同特征值的矩阵为( )
·
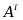
·
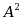
·
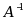
·
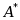
二次型 f(
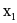 ,
,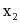 ,
,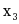 )=
)=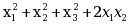 的正惯性指数为( )
的正惯性指数为( )·0
·1
·2
·3
设行列式
 =1,则行列式
=1,则行列式 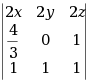 =( )
=( )·
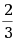
·1
·2
·

设 A,B,C 为同阶可逆方阵,则
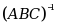 =( )
=( )·

·
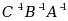
·
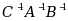
·
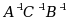
设 α 1, α 2, α 3, α 4是 4 维列向量,矩阵 A=( α 1, α 2, α 3, α 4).如果|A|=2,则|-2A|=( )
·-32
·-4
·4
·32
设 α 1, α 2, α 3, α 4 是三维实向量,则( )
·α 1, α 2, α 3, α 4一定线性无关
·α 1一定可由 α 2, α 3, α 4线性表出
·α 1, α 2, α 3, α 4一定线性相关
·α 1, α 2, α 3一定线性无关
向量组 α 1=(1,0,0), α 2=(1,1,0), α 3=(1,1,1)的秩为( )
·1
·2
·3
·4
设 A 是 4×6 矩阵,r( )=2,则齐次线性方程组 Ax=0 的基础解系中所含向量的个数是( )
·1
·2
·3
·4
设 A 是 m×矩阵,已知 Ax=0 只有零解,则以下结论正确的是( )
·m≥n
·Ax=b(其中 b 是 m 维实向量)必有唯一解
·r(A)=m
·Ax=0 存在基础解系
设矩阵 A=
 ,则以下向量中是 A 的特征向量的是( )
,则以下向量中是 A 的特征向量的是( )·
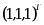
·
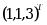
·
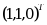
·